피타고라스 음률

피타고라스(Pythagoras, BC582?~BC497?)라는 이름을 들으면 많은 사람들이 `피타고라스의 정리’부터 떠올리는 것을 보면 피타고라스를 수학자로 인식하는 것 같다. 아닌 게 아니라 피타고라스는 ‘만물은 수다’는 주장을 펼쳤다고 하니 본인부터가 자신을 수학자로 생각했을 것 같다. 그런데 피타고라스라는 이름은 수학사에만 등장하는 게 아니다. 철학사에도 잠깐 등장하는 건 그런 대로 그렇다고 이해할 수 있는데, 서양 음악 이론의 역사를 말할 때 거의 틀림없이 피타고라스로부터 시작하는 것은 다소 의외일 수 있겠다.

최초로 음악 이론을 만든 피타고라스

피타고라스가 음악에 대한 이론(사실 소리의 높낮이에 대한 이론 정도가 맞겠지만)을 처음 만들었다는 기록은 플라톤(Plato, BC428/427~BC348/347)의 저작을 비롯해 여러 곳에 등장한다. 물론 피타고라스 이전 세대에서도 소리에 대한 이론을 알았을 거라는 증거가 없는 것은 아니나, 문헌상 증거가 부실하고 그런 이론이 후세에 영향을 주지 못했으므로 논외로 하자. 가장 유명한 기록이라 할 수 있는 것은 6세기 초의 철학자 보에티우스(Boethius, 470?~524)의 기록인데, 이에 따르면 피타고라스가 신의 안내를 받아 대장간 옆을 지나는데 듣기에 좋은 어울리는 소리가 들렸다고 한다. 그래서 알아보았더니 망치의 무게 사이에 6:8:9:12의 정수비가 성립했다는 것이다. 특히 무게가 12:6인 망치, 즉 비가 2:1인 망치를 같이 치면 높이만 다를 뿐 같은 소리, 즉, 한 옥타브 차이의 소리로 들렸다고 한다. 또한 9:6, 즉, 3:2인 경우에는 옥타브 다음으로 아름다운 음정인 완전5도(diapente) 차이의 소리로 들렸으며, 8:6이나 12:9인 경우, 즉, 4:3의 비율인 경우에는 완전4도 차이가 나는 것으로 들렸다는 것이다. 사실 실제로 위의 비율의 무게를 갖는 망치를 만들어서 간단한 실험을 하면 그런 소리 차가 나지 않는다는 것을 알 수 있으므로, 이러한 전설이 사실일 가능성은 대단히 적다. 하지만 망치의 무게 대신, 적당한 탄성을 갖는 현의 길이로 바꿔 해석하면 실제로도 상당한 근거가 있음은 잘 알려져 있다.

중세의 목판화. 첫 번째 그림에는 망치질하는 사람들이 나오며, 다른 그림에 소리에 대해 여러 가지 실험을 하는 피타고라스가 보인다.

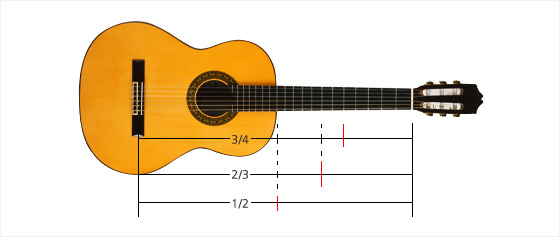
예를 들어 흔히 볼 수 있는 기타에서 기타줄의 3/4, 2/3, 1/2의 비를 갖는 곳쯤에 프렛(fret, 핑거보드에 붙여 놓은 금속조각)이 있음을 볼 수 있다. (나중에 설명하겠지만, 정확히 3/4이라는 것은 아니다.) 이 지점에 기타줄이 닿도록 하여 줄을 튕기면, 운지하지 않을 때(개방현일 때) 나는 소리보다 4도, 5도, 8도(옥타브) 높은 소리가 난다는 뜻이다.

기타 줄의 대략 3/4, 2/3, 1/2 지점에 프렛이 있다.

피타고라스는 여기서 등장하는 비율 2:1, 3:2, 4:3이 간단한 정수비라는 것에 대단히 감동했다고 한다. 5:4나 6:5 같은 정수비를 생각하지 않고 4에 그친 것은 삼각수 1, 2, 3, 4의 합 10이 완전하고 성스러운 수라는 자신의 생각에 꿰맞춘 면이 있고, 4원소설이나 4계절에서 등장하는 숫자인 4를 신비하게 본 면도 있었던 터였을 것이다. 더욱이 한 옥타브 높은 음정을 완전5도 낮추면, 그 비가 1/2를 2/3으로 나눈 3/4가 되어 완전4도가 된다는 사실 또한 자아도취할 수밖에 없는 요건이 되어, 급기야 세상의 모든 것이 수라는 주장에까지 이른 것이다. 피타고라스의 조율법: 미와 파, 시와 도 사이가 반음인 이유? 피타고라스와 그 학파는 특히 완전5도의 비율 3:2를 대단히 중요시하여, 다른 음정도 이 비율의 누적으로 설명한다. 예를 들어 완전5도로 두 번 높이면 9:4의 비율이 되는데, 이는 2:1보다 큰 비이므로, 원래 소리보다 한 옥타브 이상 높은 소리다. 따라서 이를 한 옥타브 낮춘 비율인 9:8에 해당하는 음정도 원래 음정과 비교적 조화를 이루는 소리라고 생각하고, 이를 기본 구성단위로 생각했다. 마찬가지로 완전5도로 여러 번 높이거나 낮춘 후, 원래 음과 한 옥타브 이내의 음으로 비율 조정을 하여 크기 순으로 늘어놓은 것이 이른바 7음계의 효시다. (다른 방법으로 비율 조정을 할 수도 있지만 현대 음악 이론과 비슷하도록 편의상 다음과 같은 방식으로 조정한다.)

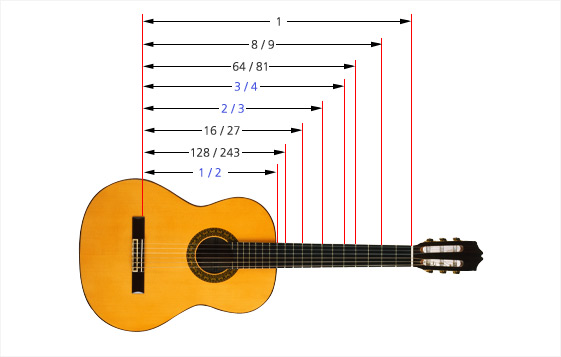
위 에서 붉은 색으로 쓴 비율과, 한 옥타브 위의 비 2를 크기 순으로 늘어놓고, 편의상 현대식 계이름을 붙여놓았다.

위와 같은 계산법에 따라 음정을 조율하는 방법을 피타고라스 조율법이라 부르는데, E와 F 사이, B와 C’ 사이를 제외하면 모두 비가 9/8로 일정함을 알 수 있다. 왜 한 옥타브는 12개의 반음으로 이루어져 있나? 사실 위와 같은 조율법은 무한 반복할 수 있다. 3/2의 거듭제곱에 2를 아무리 곱하거나 나누어도 2가 나올 수 없기 때문이다. 하지만 인간의 귀가 들을 수 있는 음정의 차는 한계가 있다. 따라서 어느 이상 음을 세분한다는 것은 의미가 없다. 실제로도 위와 같은 조율법에 따라 한 옥타브 사이에 13개의 음을 집어넣을 경우 나오는 비율은 다음과 같다.

앞서 C와 D 사이나, D와 E 사이처럼 온음이었던 구간에 파란색으로 쓴 비율이 하나씩 들어가다가, F와 G 사이에 두 개의 비율을 집어 넣어야 하므로 다소 불합리해진다. 더구나 729/512=1.4238…과, 1024/729=1.4046…의 값은 상당히 가까워 그다지 차이를 느낄 수 없다. 따라서 이쯤에서 합리적으로 타협을 하여, 1024/729를 버리고 729/512만을 취해 늘어쓰면 다음과 같다.

인접한 두 비율의 음정의 차를 반음이라 부르면, 한 옥타브를 이루는 반음의 개수가 12개다. 찬찬히 뜯어보면 2의 19제곱인 534288과, 3의 12제곱인 531441의 비가 1에 가깝기 때문에 12가 선택된 셈인데, 이 두 수의 비를 ‘피타고라스의 콤마’라 부른다. 2의 30제곱과 3의 19제곱이 비슷하기 때문에 어떤 이들은 한 옥타브를 19개의 음으로 세분하는 게 더 합리적이라고 주장하기도 한다.

피타고라스의 기타.

피타고라스 조율법의 한계 위에서 언급된 피타고라스의 콤마를 비롯하여, 피타고라스의 음악 이론은 실제 음악 연주를 하기에는 많은 문제점을 보인다. 이후의 음악 이론가들이나 실제 연주자들은 여러 가지 방법을 통해 이런 한계를 극복해나갔다. 또한 피타고라스 조율법 외에도 수학과 음악 이론이 관련 있는 부분은 더 많이 있다.