미분

함수의 그래프를 보면, 부드럽게 굽어 보이는 그래프가 많다. 사인 함수를 비롯한 삼각함수도 그렇고, 지수함수, 로그함수, 무리함수, 유리함수, 다항함수까지 보통 접하는 함수의 그래프는 대개 쭉 뻗은 직선이기보다는 부드러운 곡선이다. 그런데 이런 곡선 위의 점을 하나 골라 그 주위를 확대해보면 의외의 세상을 만나는 수가 있다. 곡선과 가장 가까운 직선- 접선

직선이 아닌 곡선 중 가장 간단한 것은 2차 함수의 그래프다. 그 중 가장 간단한 f(x)=x2의 그래프를 생각해 보자. 얼마나 간단한지, 대개 중고등학교 시절을 거치면서 무수히 그리는 경험을 한다. 이런 모양의 곡선을 포물선이라고 부르는데, 북한에서는 팔매선이라 부른다고 한다. 돌팔매질을 하면 돌이 그리는 자취가 2차 곡선의 모양이기 때문이다. 삼각함수나, 3차 함수 등이 아니고 하필 2차 곡선이어야 하는 이유도 미분과 적분으로 (공기 저항 등을 무시할 경우, 물리 법칙을 써서) 설명할 수 있는데, 그 얘기는 다음으로 미루고 여기서는 이 곡선을 확대해 보는 데 집중하기로 하자.

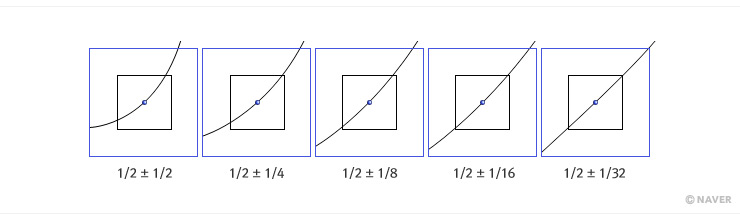
예를 들어 x=0.5를 제곱하면 0.25이다. 따라서 점 (0.5, 0.25)는 곡선 위에 있다. 이제 이 점을 중심으로 그래프를 일정 비율로 확대해 보자. 돋보기 들고, 컴퓨터 화면 확대해야겠다는 순진한 분은 없으리라 믿겠다. 예를 들어 2배, 4배, 8배, 16배, 32배 확대하면 아래 그림을 얻는다. 각 그림에서 가운데에 그린 네모를 가로, 세로 각각 두 배씩 확대하면 다음 그림이 나오도록 하였다. 점점 확대할수록 기울기가 1인 직선에 가까워지는 느낌을 받았는가?

평균 변화율과 순간 변화율 이처럼 어떤 점 (L, f(L))을 중심으로 하여 확대하면 할수록 그래프가 어떤 고정된 직선에 가까워지는 경우, (단, y 축과 나란한 직선은 제외한다) x=L에서 ‘미분 가능하다’고 말하고, 그 고정된 직선을 접선이라 부른다.  즉, 미분 가능한 점 (L, f(L))에서의 접선은 그 점 근방에서 곡선과 가장 가까운 직선으로 이해할 수 있다. 그런데 이 접선은 어떻게 구할까? 이미 접선이 지나는 점 (L, f(L))을 알고 있으므로, 기울기만 구하면 된다.

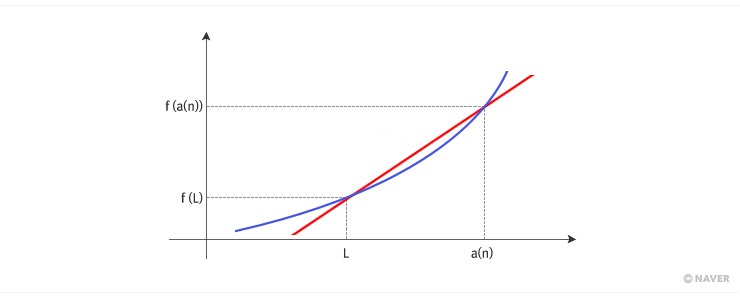
위 그림은 미분 가능한 점 (L, f(L))을 중심으로 하여 상당히 확대한 그림이라고 하자. 곡선 위의 점 (a(n), f(a(n)))은 (L, f(L))과 멀어 보이지만, 엄청나게 확대한 그림이라면 실은 꽤 가까운 점이다. 이때 미분 가능하다고 했으므로, 이 두 점을 잇는 직선과, 함수의 그래프가 대단히 가깝다고 가정하고 있다. 두 점을 잇는 직선의 기울기는 y의 변화량 f(a(n))-f(L)을 x의 변화량 a(n)-L로 나눈 값인 인데, 이 값을 두 점 (L, f(L)), (a(n), f(a(n)))의 평균 변화율이라 부른다. 구하고자 하는 접선의 기울기는, a(n)이 대단히 L에 가까울 때, 평균 변화율이 가까워지는 극한값이어야 할 것이다. 이 극한값을 L에서의 ‘순간 변화율’이라 부르는데, 다만 a(n)이 L인 경우는 애초부터 기울기를 생각할 수 없으므로 제외해야 한다. 예를 들어 f(x)=x2인 경우를 보자. a(n)이 L로 다가갈 때, 다음 극한을 생각하자는 얘기다. (다시 말하지만, a(n)은 L이 아니다.) 이고, a(n)이 L로 수렴한다고 했으므로, 극한값의 성질에 의해 이 값은 당연히 2L로 수렴한다. 따라서 x=L에서의 순간 변화율은 2L이다. L=1/2인 경우 위에서 그래프를 확대하며 짐작했던 것이 맞았음을 확인할 수 있다. 함수의 극한과 미분 계수 일반적으로 a(n) 자체는 L을 값으로 갖지 않으면서도 L로 수렴하는 모든 수열 a(n)에 대해 g(a(n))이 동일한 값 M으로 수렴할 경우, 다음과 같이 쓴다. 이런 표기를 쓰면 이제부터는 (적어도 표면적으로는) 수열을 동원하지 않고, 함수의 극한을 얘기할 수 있다. 어쨌거나 의 극한값이 존재하면 그 값이 (L, f(L))에서의 접선의 기울기라는 얘기인데, 이 값을 f’(L)이라 쓰고 ‘L에서의 함수 f의 미분계수’라 부른다. 특히 x=L에서의 접선의 방정식은 다음과 같다. 예를 들어 f(x)=x2인 경우 모든 L에 대해 f’(L)=2L임을 보였으니, x=1에서의 접선의 방정식은 다음과 같다. 항상 미분이 가능한 건 아니다 하지만 모든 함수가 미분 가능한 건 아니다. 예를 들어 그래프가 x=L에서 끊어져 있는 경우, 확대하면 직선처럼 보일 턱이 없다. 직선은 이어져 있기 때문이다. ‘간단히 말해 미분 가능하면 연속’이라 해서 속칭 ‘간미연’으로 부르는 정리인데 말로 풀어 쓰지 않고도, 수식으로 한 줄이면 증명할 수 있다. 한편 연속이더라도 미분 불가능한 경우는 많다. 예를 들어 x에 대해 절댓값을 대응하는 함수 f(x)=|x|를 생각해 보자. 이 함수의 그래프는 x=0 주변에서 제 아무리 확대해도 직선처럼 보이지 않는다. 아무리 확대해도 그 모양 그대로다. 따라서 x=0에서 미분할 수 없다는 얘기다.

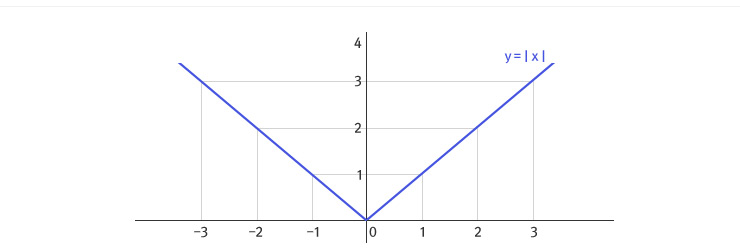
함수 f(x)=|x|는 x=0에서 미분할 수 없다.

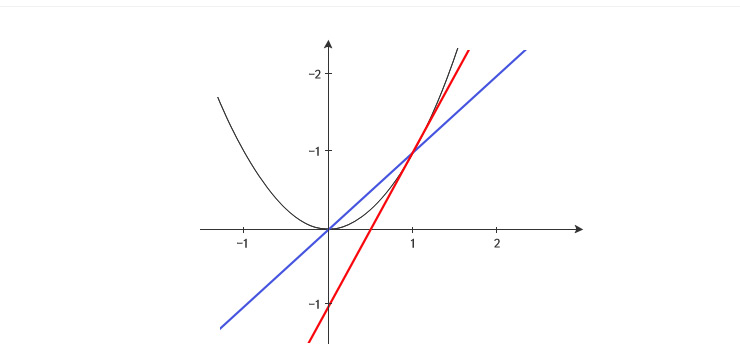
접선의 의미 - 상대 오차! 흔히 접선은 그 점 근방에서 곡선과 가장 가까운 직선이라고 말한다. 특히, x가 L 근처의 값에 가까울수록, 함숫값 f(x)와, 접선에서의 값 f(L)+f’(L)(x-L)과 가깝다. 예를 들어 보자. f(x)=x2일 때, x=1 에서 접선은 y=2x-1이었다. 따라서 x가 1 근처의 수일 때 함숫값 x2과 접선에서의 값 2x-1의 값은 가깝다. 아래에 표를 참고해보자. 예상한대로 x가 1에 가까울수록, 함숫값 f(x)와 접선에서의 값이 비슷해진다. 하지만 이렇게 이해하고만 그치면, 접선의 진정한 의미를 놓치는 수가 있다. (1,1)을 지나지만 기울기가 미분계수 2가 아니라 다른 값인 경우를 생각해 보자. 예를 들어 기울기를 1로 바꾼 직선 y=x에 대해 오차를 셈한 표는 아래와 같다. 이 경우에도 접선이었던 경우보다 오차가 크긴 하지만, x가 1에 가까울수록 오차 자체는 0에 가까워지지 않은가? 사실 다른 기울기를 아무 거나 가져오더라도 동일한 현상을 발견할 수 있다. 이래서야 곡선과 가까운 직선이라는 접선의 의미가 무엇인지 갸우뚱해지지 않을 수 없다.

f(x)=x² 그래프의 (1,1)에서의 접선 y=2x-1(붉은색)과 y=x(푸른색)의 비교

함숫값 f(x)와 접선에서의 값 f(L)+f’(L)(x-L)의 차를 절대 오차라 부른다. 사실 f’(L) 대신 다른 값 m을 대입하여 구한 절대 오차 f(x)–f(L)–m(x-L)도 x가 L 근처의 값이면 당연히 0에 가까울 수밖에 없다. 하지만, 절대 오차를 x의 변화량 x-L로 나눈 값인 상대 오차를 셈하면 얘기가 크게 달라진다. x가 L에 가까울 경우 상대 오차가 0에 가까워지는 경우는 m=f’(L)인 경우뿐이다! 증명도 한 줄에 불과하지만 왜 그런지는 직접 생각해 보길 바란다. 아무튼, 접선이란 상대 오차라는 면에서 곡선과 가까운 (유일한) 직선이라는 얘기다. 그런 의미에서 접선이 곡선과 ‘가장’ 가까운 직선이라고 말하기도 한다. 실제로 접선인 경우 다음 표에서 볼 수 있듯이, x가 L에 다가갈수록 상대 오차가 0에 가까워진다. 하지만 접선이 아닌 다른 직선인 경우에는 상대 오차가 0에 가깝지 않음을 알 수 있다. 접선을 구해서 뭐하려고? 미분은 알고 보면 별 것이 아니다. 접선을 구하자는 것이 바로 미분이기 때문이다. 물론 접선의 기울기, 즉 미분계수를 구하는 과정에서 함수의 극한, 혹은 수열의 극한을 계산해야 하는데 다소 번거로운 경우가 많아 만만한 일만은 아니다. 하지만, ‘미분법’이라 부르는 다양한 방법이 개발돼 있어, 함수의 사칙 연산, 삼각함수, 지수함수, 로그함수, 합성함수, 역함수 등을 미분하는 방법은 잘 알려져 있다. 어쨌거나, 고작 접선을 구하자고 미분을 한 거라면 실망스러운 느낌이 들 수도 있을 것 같다. 미분이 별 것인 줄 알았더니 실망스럽다며 지레짐작하지는 않길 바란다. 미분에 대해 더 알아본 다음에 판단해도 늦지 않을 테니까 말이다. 미분이 유용한 이유 몇 가지 정도는 아쉬운 대로 소개할 생각이기 때문이다.

미적분의 발견 - 변화를 분석하는 도구

어마어마한 파도가 밀려오는 장면을 애니메이션으로 만들려면 어떻게 해야 할까? 예전에는 조금씩 다른 수십 장의 그림을 빠르게 돌려 표현했다. 그러나 지금은 파도의 움직임을 방정식으로 만들어 파도 영상을 만든다. 미분을 이용해 움직이는 그림을 편하게 그릴 수 있기 때문이다. 미분의 쓰임은 그림 말고도 무수히 많다. 생활 곳곳에서 우리는 미분의 덕을 보고 있다.

변화를 분석하는 도구, 미적분의 발견.

모든 것은 움직인다 잠시 눈을 돌려 살펴보자. 우리가 살고 있는 세상은 모든 것이 움직인다. 그리고 변한다. 식물과 동물은 태어나고 성장하다가 죽는다. 날씨도 변하고 계절도 변한다. 움직이지 않는 것 같은 거대한 빌딩도 초속 약 30km의 속도로 태양을 도는 지구 위에 있으므로 사실은 움직이고 있는 셈이다. 자연만 움직이는 것이 아니라 사회도 움직인다. 사회 제도도 변하고 경제 상황도 변하고 인구도 변한다. 미분은 이처럼 움직이는 대상을 다룬다. 반면 적분은 도형의 넓이, 부피와 같이 움직이지 않는 대상을 다룬다. 미적분은 17세기에 뉴턴(Isaac Newton, 1642~1727)과 라이프니츠(Gottfried Wilhelm von Leibniz, 1646~1716)에 의해 완성됐다. 하지만 적분은 기원전부터 아이디어가 알려져 있었다. 세상의 모든 것은 움직이고 변하는데, 움직이는 대상을 연구하는 것이 왜 이렇게 늦어진 걸까? 간단한 예를 들어보자. 어떤 사람의 키를 재려고 한다. 가만히 멈추어 있을 때 재는 것과 움직이고 있을 때 재는 것 중 어느 쪽이 더 쉬울까? 움직일 때 재는 것이 훨씬 어렵다. 미분과 적분도 비슷했다. 움직이는 대상을 연구하는 미분은 17세기에 이르러서야 비로소 시작됐다.

적분은 잘라 나누고 더하기 기원전 5세기 고대 그리스의 안티폰은 원에 내접하는 정사각형을 그린 뒤, 정팔각형, 정십육각형 등 계속 변의 개수를 두 배씩 늘려나가면 원의 넓이와 똑같은 다각형을 만들 수 있다고 생각했다. 당시 사람들은 안티폰의 생각을 비판하기도 했지만 이 아이디어는 약 200년 뒤 아르키메데스(Archimedes, BC 287?~BC 212)에 의해 적분의 시작으로 인정됐다.

무수히 많은 삼각형의 넓이 합으로 포물선으로 둘러싸인 부분의 넓이를 구할 수 있다.

아르키메데스는 포물선과 같이 곡선으로 이뤄진 영역의 넓이를 구하는 방법을 알아 냈다. 구할 수 있는 삼각형으로 나눠 넓이를 구하는 방법이다. 먼저 포물선으로 이뤄진 부분의 양쪽 끝점과 가운데 점을 이어 삼각형을 만든다. 그런 다음 남은 두 부분에서도 삼각형을 만든다. 이런 과정을 반복하면 포물선으로 둘러싸인 부분의 넓이는 무수히 많은 삼각형의 넓이를 더해 구할 수 있다. 이처럼 적분은 넓이를 구하는 것에서 출발했다.

볼록한 모양 포도주 통의 부피는 많은 원기둥의 부피의 합으로 구한다.

그리고 이 적분은 17세기 초 케플러(Johannes Kepler, 1571~1630)에 의해 다시 나타났다. 케플러가 살던 때 포도주의 가격은 포도주 통 안에 막대를 넣어 포도주가 채워져 있는 높이를 재서 결정했다. 그런데 이 방법에는 문제가 있었다. 포도주를 담는 통이 배가 볼록한 모양이기 때문에 담겨져 있는 포도주의 높이와 양이 비례하지 않는다는 점이다. 예를 들어 막대로 잰 높이가 통의 1/4이라면 가격은 가득 찬 경우의 1/4이지만 통은 아래로 갈수록 좁아져 실제 포도주의 양은 통의 1/4 보다는 적다. 그래서 케플러는 어떻게 볼록한 모양의 부피를 구할지 고민했다.

정확한 포도주 통의 부피를 구하기 위해 케플러는 포도주 통을 무수히 많은 얇은 원기둥으로 잘랐다. 그런 다음 무수히 많은 원기둥의 부피를 더한다.

뉴턴과 라이프니츠의 미적분

그렇다면 미적분은 누가 발견했을까? 오래 전부터 있었던 적분 아이디어와 움직임을 연구하는 미분이 만나 미적분이라는 새로운 학문이 탄생했다. 미적분을 발견한 사람으로는 영국의 뉴턴과 독일의 라이프니츠가 동시에 거론된다. 뉴턴은 1665년부터 자신이 만든 유율법이라고 이름 붙인 미적분을 발견했다. 그리고 이를 이용해 케플러의 제2법칙과 제3법칙을 증명하는 과정에서 만유인력의 법칙을 확인했다. 행성의 움직임과 같은 물리 현상 연구에 미적분을 이용한 것이다. 한편 이보다 약간 늦은 1673년과 1676년 사이에 독일의 법률가이자 수학자인 라이프니츠도 미적분을 발견했다. 뉴턴이 운동을 분석하는 과정에서 미적분법을 발견했다면 라이프니츠는 곡선의 접선 또는 극대와 극소를 찾는 과정에서 미적분을 발견했다.

미적분은 17세기에 뉴턴(왼쪽)과 라이프니츠(오른쪽)에 의해 완성됐다.

라이프니츠가 발견한 미분을 이해하기 위해 포탄을 쏘아 올려 보자. 그리고 포탄이 그리는 곡선의 두 지점을 지나는 직선을 생각하자. 두 지점의 거리를 매우 짧게 하면 직선은 포탄이 날아가는 방향을 나타낸다. 이 직선이 수평과 평행한 곳에서 포탄의 높이가 가장 높고 이후 점점 떨어진다. 따라서 이 직선이 수평으로 된 곳을 찾기만 하면 포탄의 최고 높이를 구할 수 있다.

직선이 수평이 된 곳이 포탄의 최고 높이다.

여기서 두 점 사이의 거리를 점점 0에 가깝게 하면 직선은 사실상 곡선과 한 점에서 만난다. 이것을 접선이라고 한다. 접선이 수평인 곳에서 곡선은 그 근처에서 가장 큰 값 또는 작은 값을 갖는다. 이것을 극댓값 또는 극솟값이라고 한다. 라이프니츠는 이와 같은 곡선에 접선을 그리고, 함수의 극대와 극소를 찾는 문제를 이어받아 미적분으로 체계화 했다. 미분과 적분의 관계 사실 미분과 적분은 각각이 갖는 의미도 중요하지만 둘 사이의 관계도 중요하다. 곡선에 접선을 긋는 문제로부터 발달한 미분과 곡선으로 둘러싸인 부분의 넓이를 구하는 것에서 시작한 적분은 마치 덧셈과 뺄셈 같은 관계가 있다. 5를 더한 뒤 5를 빼면 아무 변화가 없다. 덧셈과 뺄셈은 역연산 관계기 때문이다. 마치 문을 열었다가 다시 닫으면 원래 모습이 되는 것과 같다. 마찬가지로 미분과 적분도 역연산 관계다. 어떤 함수를 적분한 뒤 미분하면 본래 함수로 되돌아 온다.

단면 사진을 찍어 전체를 파악하는 CT촬영에 적분의 원리가 들어 있다. <출처: (CC)rosiescancerfund.com at Wikipedia.org>

비슷한 시기에 서로 다른 두 나라에서 미적분을 발견했다는 점은 신기한 일이다. 그래서 오랜 기간 동안 미적분 발견의 주인공을 두고 영국과 독일이 대립했고, 학자들 사이에서도 많은 논란이 있었다. 미적분을 먼저 발견하고 역학에 이용한 사람은 뉴턴이지만 불행히도 뉴턴은 이를 발표하지 않았다. 이런 이유로 늦게 발견했지만 발표가 앞선 라이프니츠와 공방을 벌이게 된 것이다. 지금은 뉴턴과 라이프니츠를 모두 미적분의 창시자로 모두 인정하고 있는데, 현재 쓰이고 있는 미적분 기호는 라이프니츠가 만든 것이다. 수학 역사상 가장 위대한 발견으로 보아도 부족하지 않은 미적분의 발견으로, 고등 수학의 문이 열렸다. 그리고 미적분은 변화를 해석하는 강력한 무기로 우리 생활을 발전하는데 무한히 기여하고 있다.

비유클리드 기하학의 발견

운동장에 직선을 그려 보자. 직선은 곡선과 달리 곧게 똑바로 그리면 된다. 이보다 더 긴 직선은 없을까? 고속도로의 차선을 생각해 보자. 얼마나 길고 곧게 뻗은 ‘직선’인가. 그런데 그 선을 비행기에서 내려다보면 사실은 굽은 선이다. 둥근 지구 위에는 선을 아무리 똑바로 그려도 굽을 수밖에 없기 때문이다. 이처럼 직선을 그릴 수 없는 공간을 생각하다 발견한 기하학이 있다. 바로 비유클리드 기하학이다.

지구와 같은 구면체 위에 직선을 그릴 수 있을까? <출처:sxc.hu>

직선은 곧은 선?!

거인이 지구 위에 삼각형을 그린다고 생각해 보자. 거인은 막대기로 삼각형 변을 똑바로 긋는다. 그런데 아무리 똑바로 그으려고 해도 둥근 지구 위에는 애당초 직선이 존재하지 않는다. 거인은 어떻게 삼각형을 그릴까? 거인이 삼각형을 못 그릴까 봐 걱정하기 전에 우선 직선의 의미부터 되짚어 보자. 우리는 직선을 똑바로 그은 선으로 알고 있다. 이것은 자연스러운 일이다. 학교를 졸업할 때까지 책에 나오는 직선은 항상 똑바로 그은 선이고, 곡선은 구부러져 있기 때문이다. 학교에서 배운 대로 직선을 생각한다면, 책상과 같이 평평한 평면 위가 아닌 땅 위에 그린 직선을 정말 직선이라고 말할 수 있을까? 그렇지 않다. 구부러진 곡면 위에 그린 직선은 모두 직선이 아니고, 거인이 구 모양 위에 그린 삼각형은 세 내각의 합이 180°보다 커지는 일이 벌어진다. 책상 위에 직선을 그릴 때는 직선이 되지만 땅바닥에 그릴 때는 직선이 아니라면 얼마나 황당할까. 이런 고민을 처음 한 사람은 이탈리아의 수학자 사케리(Girolamo Saccheri, 1667~1733)로 알려져 있다. 사케리도 처음에는 다른 수학자들과 마찬가지로 ‘원론’을 읽으면서 도형을 연구했다. 원론은 고대 그리스의 수학자 유클리드(Euclid, BC330?~BC275?)가 남긴 도형에 대한 책으로 도형에 대한 당시까지의 연구를 집대성한 책이다. 19세기까지 수학자들은 원론으로 기하학을 연구했다. 이 책에서는 어느 점에서나 직선을 그을 수 있다고 말하지만 직선이 무엇이라는 설명은 하지 않았다. 이유는 아주 간단하다. 우리가 어떤 용어를 정의한 후에 이를 사용하려면 그 정의에 들어 있는 말을 다시 정의해야 한다.

1570년 처음 영문으로 번역된 유클리드 원론.

예를 들어 (가)라는 용어를 정의하려고 (나)라는 용어를 사용했다면, (나)라는 용어를 정의하는 데 (다)라는 용어를 사용하게 된다. 또 (다)라는 용어를 정의하려면 또 다른 용어를 사용해야 한다. 결국은 정의할 수 없는 용어가 생긴다. 그래서 유클리드는 점, 선, 면과 같은 기본 용어는 정의하지 않았다. 이런 용어를 무정의용어라고 한다. 삼각형은 세 변으로 이루어진 도형이라고 정의하지만 직선은 그냥 직선일 뿐이다. 다섯 번째 공리를 부정하라 유클리드는 무정의용어를 사용한 것과 같은 이유로 다섯 가지 공리를 정해 도형을 연구하는 출발점으로 삼았다. 공리는 약속처럼 도형을 연구할 때, 증명 없이 모두 인정하고 시작하자는 내용이다. 사케리는 이 중 마지막 공리에 의심을 품었다. 다섯 가지 공리는 다음과 같다. ① 임의의 두 점을 지나는 직선이 항상 존재한다. ② 임의의 선분은 양 끝으로 얼마든지 길이를 연장할 수 있다. ③ 한 점을 중심으로 임의의 길이를 반지름으로 하는 원을 그릴 수 있다. ④ 모든 직각은 서로 같다. ⑤ 두 직선이 한 직선과 만날 때, 같은 쪽에 있는 내각의 합이 180°보다 작으면 이 두 직선을 연장할 때 180°보다 작은 내각을 이루는 쪽에서 반드시 만난다. 네 가지 공리는 분명하고 간단한데 비해 다섯 번째 공리는 받아들이기에 너무 복잡하다. 사실 다섯 번째 공리는 직선 밖의 한 점을 지나며 이 직선에 평행한 직선은 오직 한 개뿐이라는 것과 같다. 이것을 평행선 공리라고 부른다. 원론이 발표된 이후 19세기에 이르도록 사케리뿐만 아니라 많은 수학자들은 평행선 공리를 증명하려고 노력했다.

비유클리드 기하학 중 하나인 쌍곡기하에서의 테셀레이션. 원 가장자리로 갈수록 무늬가 무한히 작아진다. <출처: Doug Dunham(University of Minnesta Duluth)>

사케리는 많은 수학자들과 다르게 다섯 번째 공리를 부정해 모순을 증명하려고 했다. 그리고 그 과정에서 새로운 정리를 많이 얻었다. 하지만 사케리는 새로운 사실을 알았음에도 불구하고 다섯 번째 공리의 모순을 얻지 못했다는 이유로 연구한 것을 모두 버렸다. 그는 새로운 기하학 발견을 문 앞에서 포기한 수학자가 된 셈이다. 그러나 독일의 가우스(Karl Friedrich Gauss, 1777~1855)와 러시아의 로바쳅스키(Nikolai Ivanovich Lobachevskii, 1792~1856), 헝가리의 보여이(János Bolyai, 1802~1860)는 새로운 생각을 했다. 가우스는 평행선 공리를 부정하면 모순이 생기는 것이 아니라 새로운 기하학이 생긴다는 것을 알아챈 최초의 사람이다. 다만 평생 동안 이를 발표하지 않아 공식적인 발견자는 아니다. 반면 보여이는 1832년 논문에서 처음으로 이 사실을 발표했고, 로바쳅스키도 1829년쯤에 이 분야에 대한 체계적인 논문을 발표하면서 새로운 기하학을 세상에 알리기 시작했다. 이들이 사케리와 다른 점은 평행선 공리를 부정하면 유클리드 기하학에 관한 지식에 모순이 생기는 것이 아니라 새로운 기하학이 생긴다는 생각을 한 점이다. 하지만 당시 이런 생각은 2000년 이상 진리로 생각했던 유클리드 기하학을 뒤엎는 생각이어서 사람들에게 인정받기까지 오랜 시간이 걸렸다.

새로운 기하학에서는 모든 것이 달라진다 비유클리드 기하학 중 구면기하학은 구의 곡면을 다루는 기하학이다. 지구를 구라고 가정했을 때 지구 표면에서 두 지점을 잇는 가장 짧은 선을 생각해 보자. 서울과 샌프란시스코 사이의 항공노선은 평면지도에서는 구부러진 곡선으로 보여 먼 거리를 돌아가는 것처럼 보이지만 지구본에서 살펴보면 최단 거리임을 확실하게 알 수 있다. 이렇게 곡면 위에서 두 점 간의 최단 거리를 측지선이라고 한다. 구면기하학에서는 직선을 구의 중심을 포함하는 대원의 둘레로 정의한다. 두 점을 잇는 최단거리인 측지선은 대원의 일부다. 이처럼 평평한 면에서 직선은 끝이 없는 곧은 선이지만, 구면기하학에서 직선은 구의 중심을 포함하는 대원이라 길이가 유한하다. 따라서 구면기하학에서 두 직선은 반드시 두 점에서 만난다.

평면과 구면에서의 직선.

이제 거인이 구면 위에 삼각형을 그린다고 상상해 보자. 볼록한 구면에서 그리는 삼각형은 평평한 평면에서 그린 삼각형과 다르다. 이때 삼각형 내각의 합은 180°보다 커진다. 또 오목한 곡면을 다루는 쌍곡면에서는 삼각형 내각의 합이 180°보다 작다. 우리는 삼각형 내각의 합을 180°로 알고 있지만 이 사실이 언제나 옳은 진리는 아닌 것이다. 한편 1854년 가우스의 제자인 리만(Georg Friedrich Bernhard Riemann, 1826~1866)은 기하학의 기초에 관한 강연을 했다. 그는 곡률이라는 개념을 도입해 다섯 번째 공리가 성립하는 공간은 곡률이 0인 공간이고 곡률이 1이면 구면처럼 평행선이 없는 공간, 곡률이 -1이면 평행선이 무수히 많은 공간이 된다는 것을 이론으로 발표했다. 나아가 곡률이 정해진 수로 나타나지 않는 공간에 대한 이론도 세웠다. 리만의 노력으로 우리는 구면이나 말안장처럼 휘어진 공간을 다룰 수 있게 됐다.

구면에서는 삼각형 내각의 합이 180°보다 크다. 반면 안장 모양의 쌍곡면에서는 삼각형 내각의 합이 180°보다 작다.

새로운 기하학이 발표된 지 약 60년 뒤, 아인슈타인(Albert Einstein, 1879~1955)은 우주가 평평하지 않고 중력에 의해서 휘어 있음을 보였다. 그리고 일반상대성이론은 공간에 대한 기초 이론을 비유클리드 기하학에서 찾았다. 이처럼 유클리드의 다섯 번째 공리에 관한 의심에서 출발한 비유클리드 기하학은 미시공간과 극대 공간을 해석하는 이론으로 폭넓게 사용되고 있다.